
The sine function, a fundamental concept in trigonometry, plays a crucial role in various scientific and engineering fields. This guide delves into the sine meaning, its mathematical definition, properties, applications, and more, providing a comprehensive understanding of this essential function.
Sine Function: Sine Meaning
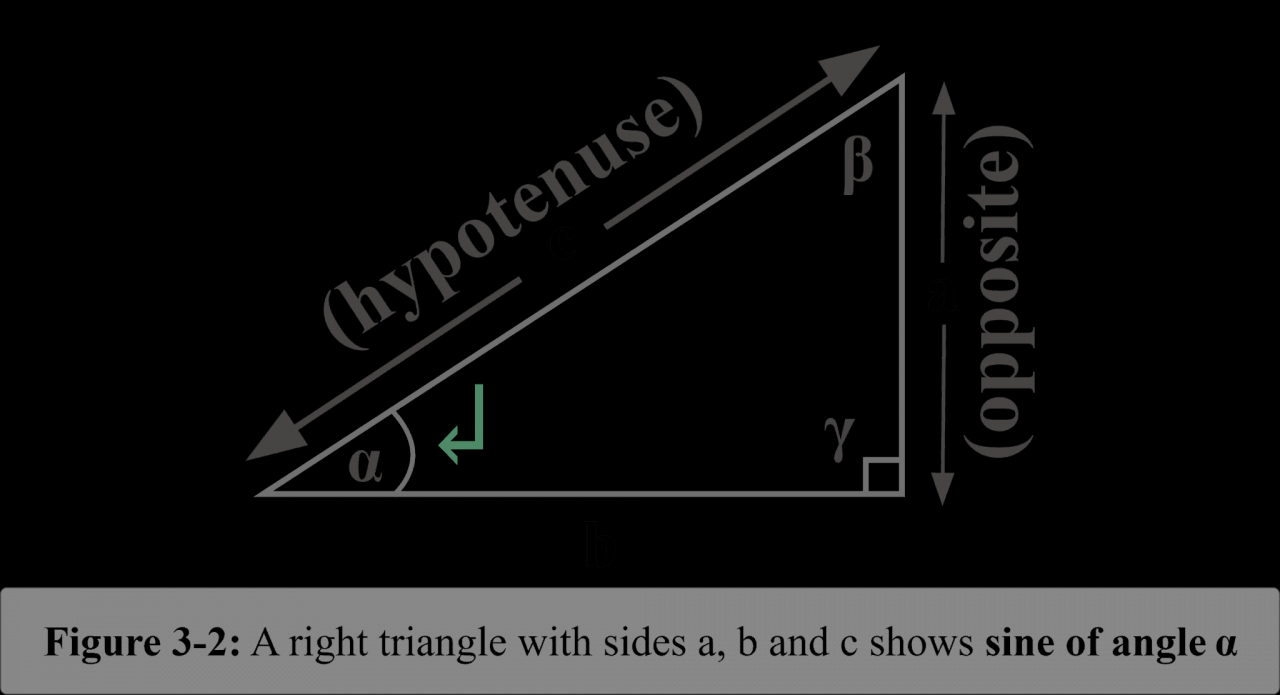
The sine function is a trigonometric function that describes the vertical component of a point moving in a circle. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
The sine function can be represented graphically as a wave that oscillates between -1 and 1. The period of the sine function is 2π, which means that it repeats every 2π units along the x-axis.
Properties of the Sine Function
- Period: 2π
- Amplitude: 1
- Domain: All real numbers
- Range: [-1, 1]
Applications of the Sine Function
- Trigonometry: Solving triangles
- Physics: Modeling periodic motion
- Engineering: Analyzing vibrations
Inverse Sine Function
The inverse sine function, also known as the arcsine function, is the inverse of the sine function. It is defined as the angle whose sine is a given number.
The inverse sine function can be calculated using the following formula:
arcsin(x) = sin-1(x) = θ
where x is the given number and θ is the angle whose sine is x.
Applications of the Inverse Sine Function, Sine meaning
- Trigonometry: Finding angles in triangles
- Navigation: Calculating the angle of elevation or depression
Hyperbolic Sine Function
The hyperbolic sine function, also known as the sinh function, is a mathematical function that is related to the sine function.
The hyperbolic sine function is defined as:
sinh(x) = (ex
e-x) / 2
where x is the input value.
Applications of the Hyperbolic Sine Function
- Mathematics: Solving differential equations
- Physics: Modeling the shape of a hanging chain
Summary
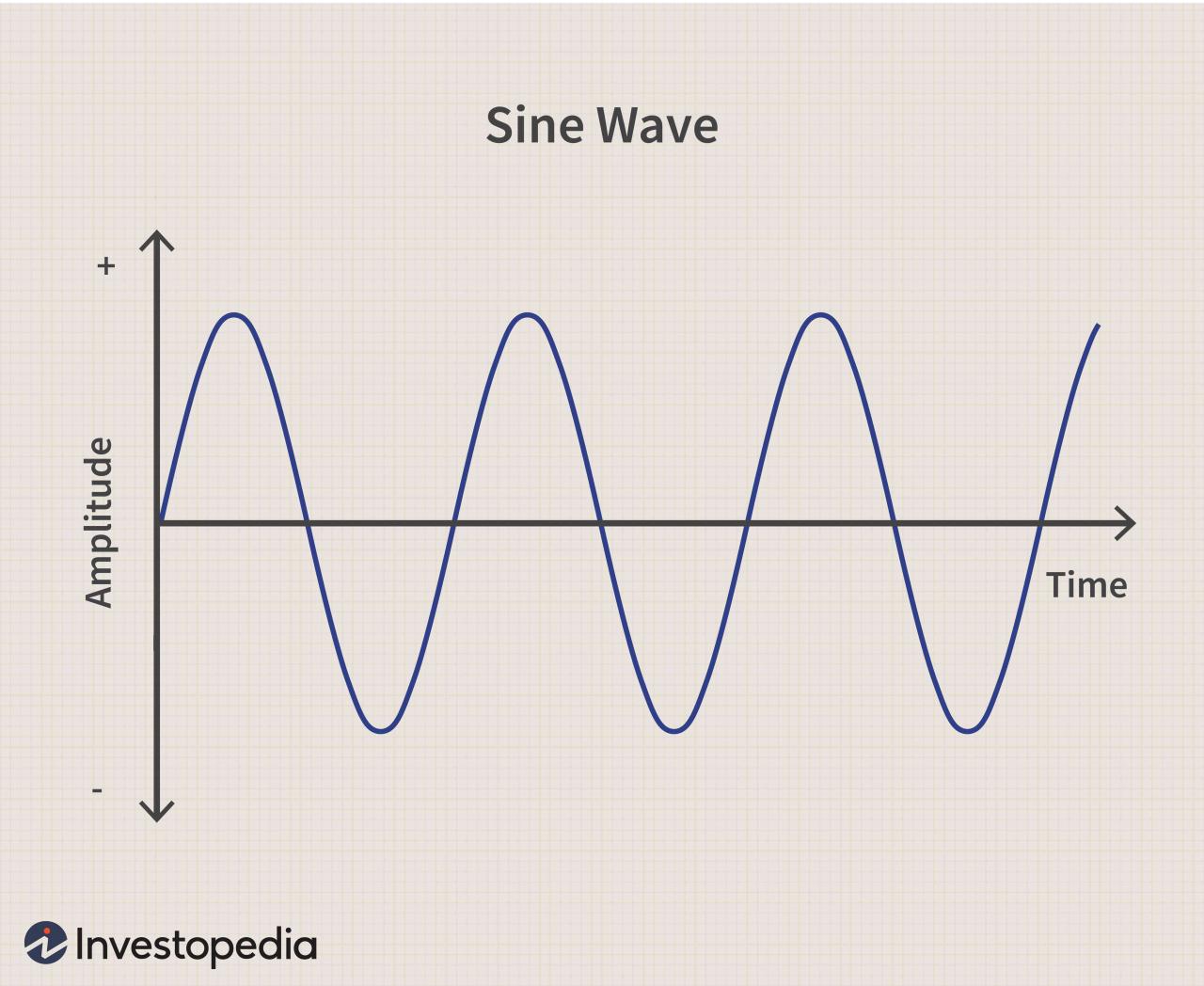
In summary, the sine function is a versatile mathematical tool with a wide range of applications. Its understanding is essential for students, researchers, and professionals in various disciplines. Whether solving triangles, modeling periodic motion, or analyzing vibrations, the sine function remains a cornerstone of mathematical analysis.
Commonly Asked Questions
What is the mathematical definition of the sine function?
The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle.
How is the sine function used in physics?
The sine function is used in physics to model periodic motion, such as the oscillation of a pendulum or the vibration of a spring.
What is the inverse sine function?
The inverse sine function, also known as the arcsine function, is the inverse of the sine function and is used to find the angle corresponding to a given sine value.





